1次関数の要点まとめ②
目次
変化の割合とはなにか
| xの増加量に対するyの増加量の割合を変化の割合といいます。 $$変化の割合=\frac{xの増加量}{yの増加量}$$ 上式を変形して, (\(y\)の増加量)=(\(x\)の増加量)×(変化の割合)もよく使われます。 |
1次関数の変化の割合
| 1次関数 \(y=ax+b\)の変化の割合は常に一定で, 傾き\(a\)に等しい。 |
言葉の基礎知識
| ・直線の式と1次関数は同じ意味です。 ・\(x=1\)のとき\(y=2\)と点(1, 2)を通るは同じ意味です。 |
傾きが等しい表現
| \(y=cx+d\)に平行な直線の傾きは\(c\)です。 変化の割合が\(c\)である直線の傾きは\(c\)に等しいです。 |
\(y\)切片が等しい表現
| \(y=cx+d\) と直線が\(y\)軸上の1点で交わるとき, \(y\)切片の値は\(d\)になります。 |
2点を通る直線の式
| 2点\((x_1, y_1), (x_2, y_2)\)が与えられている直線の式を求める際には, 傾きを最初に計算します。 直線の傾き\(=\displaystyle\frac{yの増加量}{xの増加量}\) であるから, \(a=\displaystyle\frac{y_2-y_1}{x_2-x_1}\)で求めることができます。 |
変域
| xのとりうる値の範囲のことをxの変域といいます。 同様に, yのとりうる値の範囲のことをyの変域といいます。 通常, 問題を解く際には, xの変域が示されていて, yの変域を求めていきます。 |
変域の表し方
| \(x\)が\(m\)以上\(n\)以下の値をとるときには, \(m≦x≦n\)と表します。 |
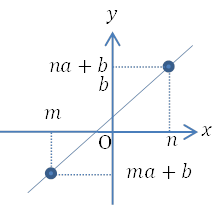
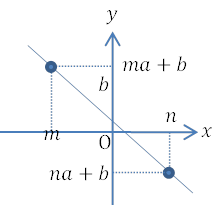
\(y\)の変域
| \(y=ax+b\)の \(x\) の変域が \(m≦x≦n\) のときの\(y\)の変域は, 直線が右上がりか右下がりかによって変わります。 すなわち, \(a>0\)のとき, \(ma+b≦y≦na+b\) \(a<0\)のとき, \(na+b≦y≦ma+b\) |