相似な図形の面積比と体積比の関係
△ABCと△DEFの相似比が1:2であるとします。このとき, △ABCと△DEFの面積比はどうなっているのでしょうか。 △ABC∽△DEFであるので, BC:EF=1:2であるから, EF=2BC また, AH:DI=1 […]
角の二等分線と線分比
△ABCで, ∠Aの二等分線と辺BCの交点をDとすると,AB:AC=BD:CDである。 証明には二等辺三角形を利用するために, ADに平行な補助線をひくことがポイントです。 ∠BACの二等分線と辺BCの交点をDとする。点 […]
中点連結定理を使った証明問題
中点連結定理 △ABCの2辺AB, ACの中点をそれぞれD, Eとするとき,DE∥BC かつ DE\(=\displaystyle\frac{1}{2}\)BC 右の図のように, △ABCの内部に点Dをとり, 辺AB, […]
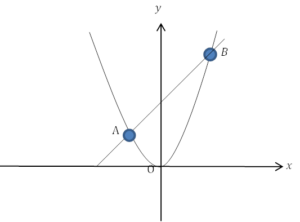
放物線と直線の交点について
放物線と直線が交わる問題について解説していきます。 1 点A, Bの\(x\)座標がともにわかっている場合 例 関数\(y=x^2\)のグラフ上に2点A, Bがあり, A, Bの\(x\)座標が-2, 3であるとき, 点 […]
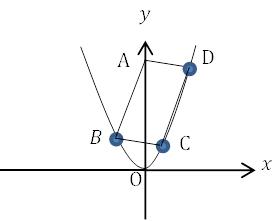
平行四辺形と放物線の座標の求め方
平行四辺形と放物線の問題について解説していきます。 高校入試レベルにおける平行四辺形と放物線の問題は, 1点が\(y\)切片上にあり, 残り3辺が放物線上にある問題を扱っていきます。このときパターンは大きく2つあります。 […]
複雑な連立方程式の計算
小数がある連立方程式の解き方 \begin{cases}0.3x+0.2y&=0.7・・・①\\0.01x+0.05y&=0.03・・・②\end{cases}のような問題を解くときには, 小数があると計 […]
1次関数の要点まとめ②
変化の割合とはなにか xの増加量に対するyの増加量の割合を変化の割合といいます。 $$変化の割合=\frac{xの増加量}{yの増加量}$$ 上式を変形して, (\(y\)の増加量)=(\(x\)の増加量)×(変化の割合 […]