立体の表面積
目次
立体の表面積
立体の表面積を求めるには, 展開図を描いて, 底面積と側面積を求めて和を出します。
三角柱の表面積
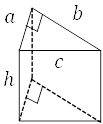
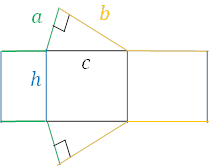
底面は, 底面\(a\), 高さ\(b\) の直角三角形です。側面は, 縦\(h\), 横\(a, b, c\)の長方形です。
底面積は, \((a×b÷2)×2=ab\)
側面積は, \(h×a+h×b+h×c=h(a+b+c)\)
よって, 三角柱の表面積\(=\)底面積+側面積\(=ab+h(a+b+c)\)
円柱の表面積
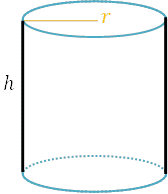
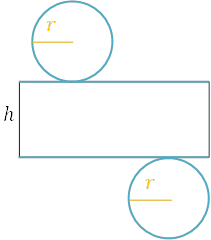
底面は, 半径\(r\)の円が2つ, 側面は縦\(h\), 横は底面の円の周の長さです。
底面積\(=\pi×r×r×2=2\pi r^2\)
側面積\(=h×2\pi r=2\pi hr\)
表面積=底面積+側面積\(=2\pi r^2+2\pi hr=2\pi r(r+h)\)
円錐の表面積
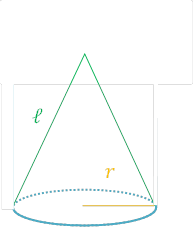

底面は半径\(r\)の円が1つ, 側面は半径が母線\(ℓ\)周の長さが底面の円の周の長さのおうぎ形です。
底面積\(=\pi r^2\)
側面積は半径×おうぎ形の弧の長さ÷2であるから, おうぎ形の弧の長さ=底面の円周の長さより,
側面積\(=ℓ×2\pi r÷2=\pi ℓr\)
よって, 表面積\(=\pi r^2+\pi ℓr=\pi (r+ℓ)\)
球の表面積
球の表面積は, その球の中心を通る平面で切ったときの切り口の円の面積の4倍になることがわかっています。球の展開図は通常考えません。また, 導出には高校数学の知識を要するので, ここでは結果のみを示します。導出法を知りたい場合は, 高校数学の積分を学習してみてください。
半径\(r\)の球の表面積Sは, \(S=4\pi r^2\)
