放物線と直線の交点について
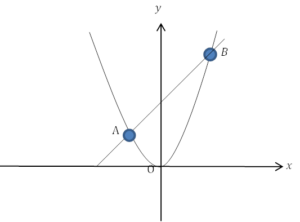
放物線と直線が交わる問題について解説していきます。 1 点A, Bの\(x\)座標がともにわかっている場合 例 関数\(y=x^2\)のグラフ上に2点A, Bがあり, A, Bの\(x\)座標が-2, 3であるとき, 点 […]
平行四辺形と放物線の座標の求め方
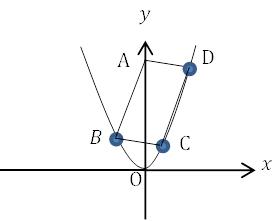
平行四辺形と放物線の問題について解説していきます。 高校入試レベルにおける平行四辺形と放物線の問題は, 1点が\(y\)切片上にあり, 残り3辺が放物線上にある問題を扱っていきます。このときパターンは大きく2つあります。 […]
座標平面上の2点間の距離の求め方
座標平面上の2点間の距離の求め方 2点を結ぶ線分を斜辺とし, \(x\)軸に平行な辺と\(y\)軸に平行な辺をもつ直角三角形をつくり, 三平方の定理を使います。2点A\((a, b), B(c, d)\)間の距離ABにつ […]
特別な直角三角形の辺の比の関係について
直角三角形の中でも特に2つの三角形を紹介していきます。今は使っていない人もいるかもしれませんが, 三角定規の2組が特別な角度をもっています。 3つの角度が30°, 60°, 90°の直角三角形 3つの角度が30°, 60 […]
重心の性質を中点連結定理を使って証明する
△ABCの各辺の中点をD, E, Fとし, BE, CFを結びます。このとき, AD, BE, CFが1点Gで交わることを証明しなさい。また, 線分AD, BE, CFがGによって, 2:1に分けられることを証明しなさい […]
式の計算の利用~数の性質編~
数の表し方 ・偶数は整数 \(n\) を用いて, \(2n\) と表すことができます。 ・奇数は偶数に1を加えた数とみなし, 整数\(n\)を用いて, \(2n+1\)と表すことができます。 ・連続する3つの整数は, […]
式の計算の利用~計算を楽にする~
例えば \(71×71\) はいくつになるでしょうか。筆算を使えば計算できるでしょうが, 暗算をするとなると少し難しいと思います。また, \(75^2-25^2\) は多少計算が大変です。 これをもっと速く簡単に計算でき […]
中点連結定理について徹底解説
中点連結定理 △ABCの2辺AB, ACの中点をそれぞれD, Eとするとき,DE∥BC かつ DE\(=\displaystyle\frac{1}{2}\)BC △ABCの辺AB, AC上の中点をそれぞれD, Eとすると […]