放物線と直線の交点について
2021年11月29日
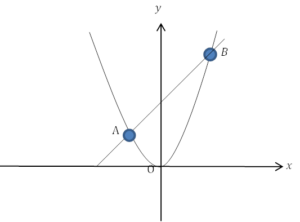
放物線と直線が交わる問題について解説していきます。 1 点A, Bの\(x\)座標がともにわかっている場合 例 関数\(y=x^2\)のグラフ上に2点A, Bがあり, A, Bの\(x\)座標が-2, 3であるとき, 点 […]
平行四辺形と放物線の座標の求め方
2021年11月28日
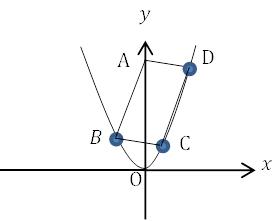
平行四辺形と放物線の問題について解説していきます。 高校入試レベルにおける平行四辺形と放物線の問題は, 1点が\(y\)切片上にあり, 残り3辺が放物線上にある問題を扱っていきます。このときパターンは大きく2つあります。 […]
1次関数の要点まとめ②
2021年11月25日
変化の割合とはなにか xの増加量に対するyの増加量の割合を変化の割合といいます。 $$変化の割合=\frac{xの増加量}{yの増加量}$$ 上式を変形して, (\(y\)の増加量)=(\(x\)の増加量)×(変化の割合 […]