円順列

青玉2個,　黄玉2個,　緑2個の6個を円形に並べたときの総数を求めなさい。

青玉１つを固定すると,　残りの青玉の位置は,　次のように場合分けをすることができる。

(ⅰ)　固定した青玉と隣り合わせになる場合

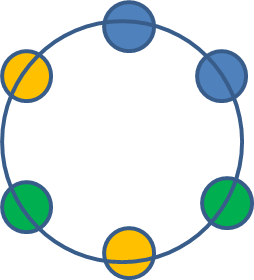
残りの黄玉2個と緑玉2個の並べ方を考えればよいから,　重複順列より,

\(\displaystyle\frac{4!}{2!2!}=6\)(通り)

(ⅱ)　固定した青玉との間に緑または黄の玉が１つ存在する場合

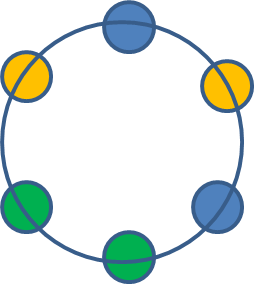
仮に黄玉1つが青玉との間にあるとき

黄玉1個と緑玉2個の並べ方を考えればよいから,　重複順列より,

\(\displaystyle\frac{3!}{2!}=3\)(通り)

緑玉のときも同様であるから,　3×2=6(通り)

(ⅲ)　固定した青玉の向かい側にある場合

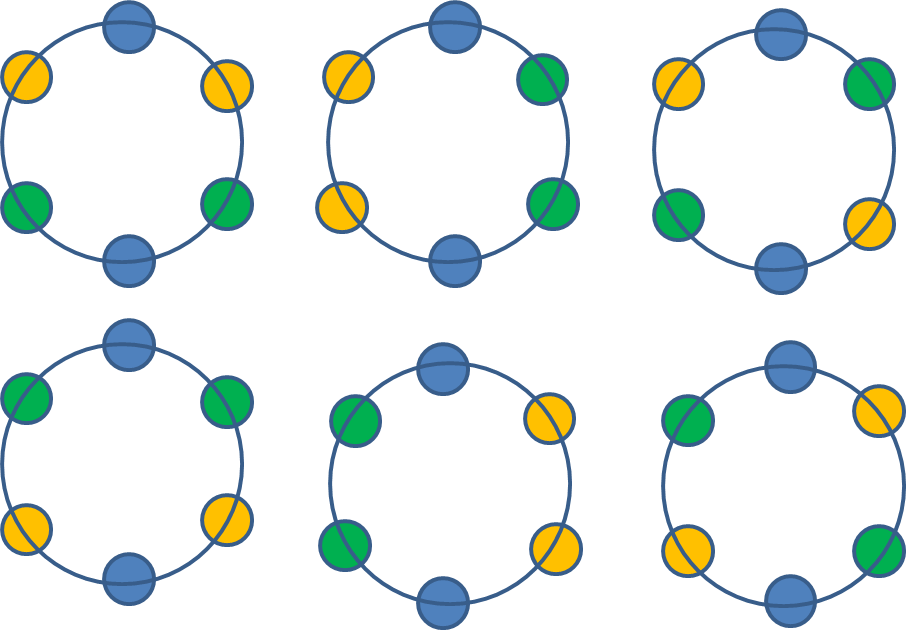
緑玉と黄玉の並べ方6通りのうち,　左右対称なものが2組あり,　180°回転すると一致するものがあるので,

\(\displaystyle\frac{4}{2}+2=4\)(通り)

　

(ⅰ)(ⅱ)(ⅲ)より6+6+4=16(通り)