平行四辺形と放物線の座標の求め方

平行四辺形と放物線の問題について解説していきます。

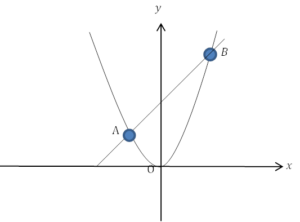
高校入試レベルにおける平行四辺形と放物線の問題は,　1点が\(y\)切片上にあり,　残り3辺が放物線上にある問題を扱っていきます。このときパターンは大きく2つあります。

1　\(x\)軸に平行な辺がある場合　

2　\(x\)軸に平行な辺がない場合

この2つについて解説を行っていきます。

1　\(x\)軸に平行な辺がある場合　

　

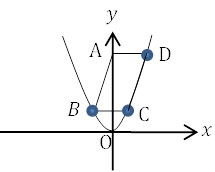
A→D→B・Cの順に座標を求めていきます。

例　平行四辺形ABCDで,　頂点Aは\(y\)軸上にあり,　B,　C,　Dは関数\(y=x^2\)のグラフ上にある。また,　点Dのx座標は正であり,　辺BCは\(x\)軸に平行である。Aの座標が(0,　16)のとき,　点B,　C,　Dの座標を求めなさい。

まず,　最初に点Dの座標が簡単に求まります。辺ADは\(x\)軸に平行であるから,　点Dの\(y\)座標は点Aの\(y\)座標は同じです。

よって,　点Dの\(y\)座標は16です。点Dは\(y=x^2\)にあることから,　代入することにより,　\(x\)座標を求めることができます。

\(16=x^2\)より,　\(x=\pm4\)となりますが,　問題文にある条件により,　\(x\)座標は正なので,　\(x=4\)　

よって,　点D(4,　16)と求める事ができます。

今度は,　BとCの座標ですが,　辺BCは\(x\)軸に平行なので,　BとCの\(y\)座標は同じです。

また,　BとCの両方とも\(y=x^2\)上にあるから,　\(y\)座標が同じとき,　点Bと点Cの\(x\)座標は絶対値が等しく,　符号が反対になります。

これより,　辺BCの中点は\(y\)軸上にあることがわかります。　

辺BCの長さは辺ADと等しく,　４なので,　4÷2＝2で,　点Bのx座標は\(-2\),　点Cの\(x\)座標は2とわかります。

\(y=x^2\)に代入して,　\(y=4\)を得るので,　点B\((-2,　4)\),　点C\((2,　4)\)

例　平行四辺形ABCDで,　頂点Aは\(y\)軸上にあり,　B,　C,　Dは関数\(y=ax^2\)のグラフ上にある。また,　点Dのx座標は正であり,　辺BCは\(x\)軸に平行である。Aの座標が(0,　\(p\))のとき,　点B,　C,　Dの座標を求めなさい。

攻略の手順 1　点A\((0,　p)\)であるから,　点Dの\(y\)座標は\(p\) 2　\(p=ax^2\)を解いて,　\(x=\displaystyle\frac{\sqrt{ap}}{a}\)　よって,　点D\((\displaystyle\frac{\sqrt{ap}}{a} ,　p)\) 3　AD＝ \(\displaystyle\frac{\sqrt{ap}}{a}\) より,　辺BC＝ \(\displaystyle\frac{\sqrt{ap}}{a}\) 。　辺BCの中点は\(y\)軸上にあるから,　点B,　Cの\(x\)座標はそれぞれ\(- \displaystyle\frac{\sqrt{ap}}{2a} ,　 \displaystyle\frac{\sqrt{ap}}{2a} \) 4　\(y=ax^2\)に代入して,　\(y= \displaystyle\frac{p}{4}\)

2　\(x\)軸に平行な辺がない場合

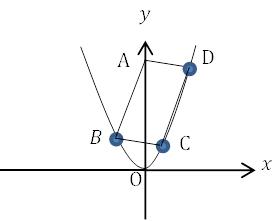
Oは原点,　A,　B,　Cは関数\(y=x^2\)のグラフ上の点で,　四角形ABCDは平行四辺形である。点A,　点Dの座標がそれぞれ\((-2,　4),　(0,　12)\)のとき,　点Cの座標を求めなさい。

\(x\)軸,　\(y\)軸に平行でない辺の長さを直接求めるのは計算が少し大変ですが,　相似の性質を使うことによって,　対辺が等しいことは\(y\)座標または\(x\)座標の差が等しいことに置きかえることができます。平行四辺形の性質による示し方は何通りかありますが,　このうち2つを紹介していきます。

1　平行四辺形の対辺が平行でその長さが等しいことを利用した解き方

ADの傾きは,　\(\displaystyle\frac{12-4}{0-(-2)}=4\)

B\((b,　b^2),　C(c,　c^2)\)とおくと,　BCの傾きは,　

\(\displaystyle\frac{c^2-b^2}{c-b}=\displaystyle\frac{(c+b)(c-b)}{c-b}=c+b \)

よって,　\(c+b=4\)・・・①

また,　点Aと点Dの\(y\)座標の差は,　8であるから,　

点Cと点Bの\(y\)座標の差も8になります。よって,　\(c^2-b^2=8\)

すなわち,　\((c+b)(c-b)=8\)

①より,　\(c－b=2\)・・・②

①,　②を連立させて,　\(b=1,　c=3\)が得られます。

よって,　点B(1,　1),　点C(3,　9)

2　平行四辺形の中点はそれぞれの中点で交わることを使った解き方

これが一番簡単かもしれません。同様に,　 B\((b,　b^2),　C(c,　c^2)\) とおくと,

ACの中点は,　\((\displaystyle\frac{c-2}{2},　\displaystyle\frac{c^2+4}{2})\)

DBの中点は,　 \((\displaystyle\frac{b+0}{2},　\displaystyle\frac{b^2+12}{2})\)

これが等しいので,　

\(\displaystyle\frac{c-2}{2}=\displaystyle\frac{b+0}{2}\)かつ,　\(\displaystyle\frac{c^2+4}{2}= \displaystyle\frac{b^2+12}{2}\)

すなわち,　\(b=c-2,　c^2=b^2+8\)　これを解いて,　\(b=1.　c=3\)

よって,　点B(1,　1),　点C(3,　9)

いかがでしたでしょうか。他にもやり方があるので探してみてくださいね！