平行四辺形の定義と性質

平行四辺形の定義

2組の対辺が平行な四角形を平行四辺形といいます。

平行四辺形の性質

平行四辺形は以下のような性質があります。 1　2組の対辺の長さが等しい 2　2組の対角の大きさが等しい 3　2つの対角線はそれぞれの中点で交わる

平行四辺形の性質の証明

平行四辺形の定義を利用して性質を証明していきます。なお,　一度証明された性質は次の証明で用いることができます。

1　2組の対辺の長さが等しいことの証明

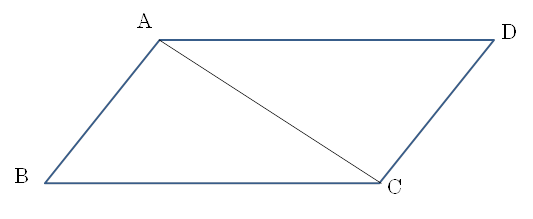
平行四辺形ABCDの点Aと点Cを結びます。△ABCと△CDAにおいて, 共通な辺だから,　AC=CA・・・① 定義よりAD∥BCであるから,　平行線の錯角は等しいので, ∠BAC＝∠DCA・・・➁ ∠BCA＝∠DAC・・・③ ➀,　➁,　③より,　1組の辺とその両端の角がそれぞれ等しいので,　△ABC≡△CDA 対応する辺は等しいので,　AB＝CD,　BC＝DA よって,　2組の対辺が等しいことが示されました。

2　 2組の対角の大きさが等しいことの証明

∠BADと角BCDは2つの角の和で表すことができます。 ∠BAD＝∠BAC＋∠DAC ∠BCD＝∠BCA＋∠DCA ➁を用いると,　∠BAD＝∠DCA＋∠DAC・・・④ ③を用いると,　∠BCD＝∠DAC＋∠DCA・・・⑤ ④,　⑤より,　∠BAD＝∠BCD・・・⑥ また,　△ABC≡△CDAより,　対応する角は等しいので, ∠ABC＝∠CDA・・・⑦ ⑥,　⑦より,　2組の対角が等しいことが示されました。

3　2つの対角線はそれぞれの中点で交わる ことの証明

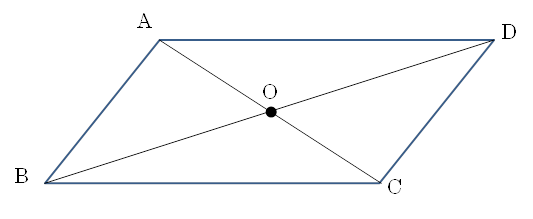
点Bと点Dを結び,　ACとの交点をOとする。示したいのはAO=COかつBO=DOである。 この2辺を含む三角形は△ABOと△CDOなので,　この2つの三角形の合同を示していきます。 △ABOと△CDOにおいて, 平行四辺形の対角は等しいので,　AB=CD・・・⑧ AB∥BCより,　平行線の錯角は等しいので, ∠BAO＝∠DCO・・・⑨ ∠ABO＝∠CDO・・・⑩ ⑧,　⑨,　⑩より,　1組の辺とその両端の角がそれぞれ等しいので, △ABO≡△CDO 対応する辺は等しいので, AO=CO,　BO＝DO よって,　2つの対角線はそれぞれの中点で交わることが示されました。

まとめ

長さや角度が等しいことの証明には三角形の合同を示すことが重要です。ただし,　そのままだと三角形がないことがあるので,　補助線をうまくひいて三角形をつくるようにしていきましょう！

わからないところがありましたらコメントで聞いていただければと思います！