放物線と線分の長さ
点A\((a_1, a_2)\)と点B\((b_1, b_2)\)間の長さは三平方の定理を学習することによって求めることができますが, 現時点ではまだ求めることができません。しかし, このうちの特殊な例, すなわち, このうちの\(x\)座標または\(y\)座標が等しい2つの点同士の長さは求めることができます。それを解説していきます。
点A, Bなどの\(x\)座標を文字で表すときは, 分かりやすいように, \(a, b\)のように置きますが, 点Pの\(x\)座標を表すときには\(t\)を使うことが多いです。もちろん他の文字も可能ですが, 通例的に文字は揃えたほうがいいでしょう。
目次
\(x\)座標が等しいとき
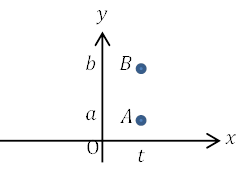
点A\((t, a)\)と点B\((t, b)(a<b)\)は\(x\)座標が等しいので, ABの長さは\(y\)座標の大きい方から小さい方を引くことによって求めることができます。
線分ABの長さ\(=b-a\)
\(y\)座標が等しいとき
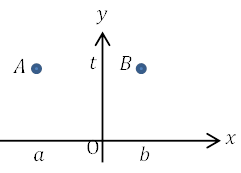
点A\((a, t)\)と点B\((b, t)(a<b)\)は\(y\)座標が等しいので, ABの長さは\(x\)座標の大きい方から小さい方を引くことによって求めることができます。
線分ABの長さ\(=b-a\)
座標平面上での扱い
座標平面上では, 平行という言葉がキーワードです。
\(x\)軸に平行な直線→直線上の2点の\(y\)座標は等しい
\(y\)軸に平行な直線→直線上の2点の\(x\)座標は等しい
と考えます。
特に, \(x\)軸に平行な直線が同一放物線は次の性質があります。
放物線は\(y\)軸に関して対称であるので, 放物線上にある点同士は, \(y\)座標が等しく, \(x\)座標の 絶対値が同じで符号が異なるものとなります。
すなわち, 点Aと点Bが\(x\)軸に平行であるとき, Aの座標を\((a, a^2)\)とおくと, B\((-a, a^2)\)となります。
これを利用して正方形が題材となる問題があります。それを見ていきましょう。
正方形を利用した問題の解き方
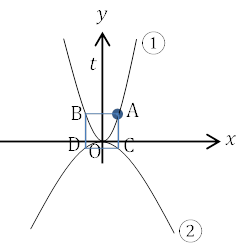
| ①は関数\(y=2x^2\), ②は関数\(y=-x^2\)のグラフである。①のグラフ上に点Aをとり, 点Aの\(x\)座標を\(a(a>0)\)とする。Aを通り\(x\)軸に平行な直線と①のグラフが交わる点でA以外の点をBとし, Aを通り\(y\)軸に平行な直線と②のグラフとの交点をCとする。さらに, 点Cを通り\(x\)軸に平行な直線と②のグラフが交わる点でC以外の点をDとして, 四角形ABCDをつくる。四角形ABCDが正方形になるとき, 点A, B, C, Dの座標を求めなさい。 |
点Aの\(x\)座標が\(a\)とわかっているので, Aの座標がわかります。
①上に点Aがあるので, \(y=2×a^2=2a^2\) よって, 点A\((a, 2a^2)\)とわかります。
ABは\(x\)軸に平行なので, 点Bの\(y\)座標は点Aと同じになります。また, 点Aと同じ①上にあるので,
\(x\)座標はAの\(x\)座標と絶対値が同じで符号が異なります。よって, 点B\((-a ,2a^2)\)
また, ACは\(y\)軸に平行なので, CはAの\(x\)座標と同じになります。
Cは②上にあるので, \(y=-a^2\) よって, 点C\((a, -a^2)\)
Bの考え方と同様に, 点D\((-a, -2a^2)\)とわかります。
四角形ABCDは対辺が\(x\)軸, \(y\)軸に平行であるから, 4つの角度は等しいです。また, 平行四辺形でもあるので, 長方形であることはわかっています。
なので, 4つの辺が等しいすなわち, AB=ACであれば正方形になります。
ABの長さは\(x\)座標の差で求めることができます。AB\(=a-(-a)=2a\)
ACの長さは\(y\)座標の差で求めることができます。AC\(=2a^2-(-a^2)=3a^2\)
AB=ACを解きます。 \(2a=3a^2\)であるから, \(3a(a-\displaystyle\frac{2}{3})=0\)
\(a>0\)であるから, \(a=\displaystyle\frac{2}{3}\)
よって, A\((\displaystyle\frac{2}{3}, \displaystyle\frac{8}{9})\), B\((-\displaystyle\frac{2}{3}, \displaystyle\frac{8}{9})\)
C\((\displaystyle\frac{2}{3}, -\displaystyle\frac{4}{9})\), D\((-\displaystyle\frac{2}{3}, -\displaystyle\frac{4}{9})\)