放物線と直線の交点について

放物線と直線が交わる問題について解説していきます。

1　点A,　Bの\(x\)座標がともにわかっている場合

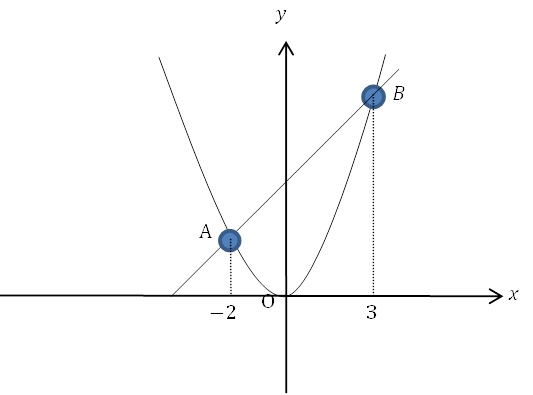
例　関数\(y=x^2\)のグラフ上に2点A,　Bがあり,　A,　Bの\(x\)座標が－2,　3であるとき,　点A,　Bの座標と,　直線ABの式を求めなさい。

点A,　Bは関数\(y=x^2\)上にあるので,　\(x=-2,　3\)をそれぞれ代入することにより,　\(y\)座標を求めることができます。

\(x=-2\)のとき,　\(y=(-2)^2=4\)

\(x=3\)のとき,　\(y=3^2=9\)

よって,　点A\((-2,　4)\),　点B\((3,　9)\)

直線の式を求めるために,　\(y=ax+b\)に2点を代入してもいいですが,　傾きを出すほうが簡単なので,　そちらのやり方で求めます。

ABの傾きは,　\(\displaystyle\frac{9-4}{3-(-2)}=1\)

傾きが1であるから,　ABの直線の式は,　\(y=x+b\)とおけます。

点Bを通るので,　\(9=3+b,　b=6\)

よって,　直線ABの式は,　\(y=x+6\)　

2　点A,　Bの\(x\)座標のうち一方がわかっている場合

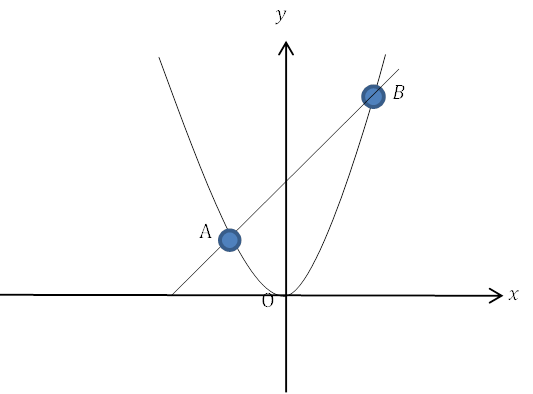
例　関数\(y=ax^2\)と関数\(y=x+6\)のグラフが2点A,　Bで交わっている。点Aの\(x\)座標が\(-2\)である。このとき,　点Bの座標を求めなさい。

点Aの\(x\)座標と,　直線の式がわかっているので,　点Aの\(y\)座標がわかります。

\(y=-2+6=4\)より,　点A\((-2,　4)\)

関数\(y=ax^2\)上に点Aがあるので,　\(4=a×(-2)^2\)

よって,　\(a=1\)がわかるから放物線は,　\(y=x^2\)とわかります。　

点Bは2つの関数上にあるので,　2つの関数を連立させて2次方程式を解いていきます。

関数\(y=x^2\)と\(y=x+6\)を連立させると,

\(x^2=x+6\)　すなわち,　\(x^2-x-6=0\)

\((x-3)(x+2)=0\)を解いて,　\(x=-2,　3\)　

点Aの\(x\)座標は\(-2\)であるから,　点Bの\(x\)座標は3,　よって,　点B\((3,　9)\)

3　点A,　Bの\(x\)座標がともにわかっていない場合

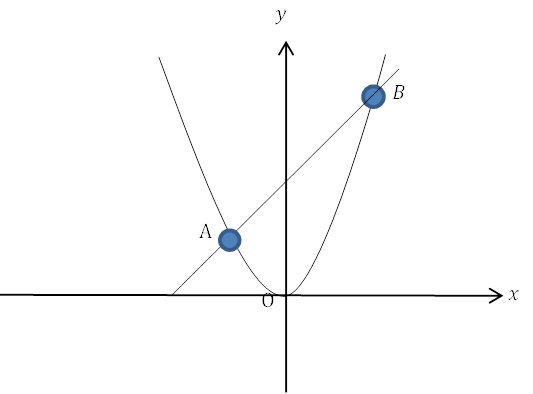
例　 関数\(y=x^2\)と関数\(y=x+6\)のグラフが2点A,　B(ただし,　Aの\(x\)座標\(<\)Bの\(x\)座標)で交わっている。点A,　Bの座標を求めなさい。

点A,　Bは2つの関数上にあります。この2つの交点を求めるためには,　2つの関数を連立させて2次方程式を解いていきます。

関数\(y=x^2\)と\(y=x+6\)を連立させると,

\(x^2=x+6\)　すなわち,　\(x^2-x-6=0\)

\((x-3)(x+2)=0\)を解いて,　\(x=-2,　3\)　

よって,　点A\((-2,　4)\),　点B\((3,　9)\)