角の二等分線と線分比
| △ABCで, ∠Aの二等分線と辺BCの交点をDとすると, AB:AC=BD:CDである。 |
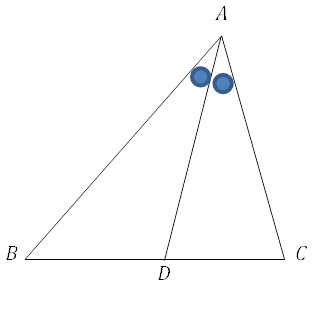
証明には二等辺三角形を利用するために, ADに平行な補助線をひくことがポイントです。
∠BACの二等分線と辺BCの交点をDとする。点Cを通り, 辺DAに平行な直線をひき, 直線BAとの交点をEとします。
| 角の二等分線より, ∠BAD=∠CAD・・・① 作図により, AD∥ECであるから, 平行線の同位角は等しいので, ∠BAD=∠AEC・・・② 平行線の錯角は等しいので, ∠CAD=∠ACE・・・③ ①, ②より, ∠CAD=∠AEC・・・④ ③, ④より, ∠AEC=∠ACE・・・⑤ ⑤より, 2つの角が等しいので, △ACEは二等辺三角形である。 よって, AC=AE・・・⑥ △BECで, AD∥ECであるから, AB:AE=BD:CD・・・⑦ ⑥, ⑦より, AB:AC=BD:CDが示されました。 |
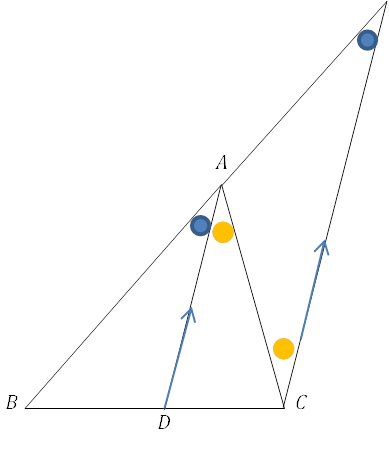
⑦では平行線と線分の比の関係を利用しました。二等分線の性質は今後多く出てくるので, しっかり理解していきましょう。
これが分かるようになることで, 以下の長さがわかります。
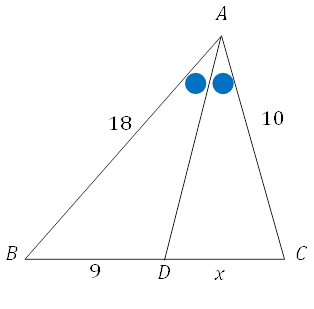
図のDCは, AB:AC=BD:DCの関係があるので,
18:10=9:DC すなわち, 18×DC=10×9より, DC=5とわかります。
以上です。いかがでしたでしょうか。
