関数とは何か
目次
変数
| \(x, y\)のように, いろいろな値をとる文字のことを変数といいます。一方, 2や\(-3\)のように, 一つの値のみをもつ数を定数といいます。 |
関数
| \(x\)の値を決めると, それに対応して\(y\)の値がただ1つ決まるとき, \(y\)は\(x\)の関数であるといいます。 このとき, 式で表すと, \(y=(x\)を含む文字式)の形になります。 |
関数の具体例
関数の言葉の意味を見ても, よくわからないと思いますので, 次の文章を例に, 関数とは何かについての理解を深めていきましょう。
| 次のうち, \(y\)が\(x\)の関数であるのはどれか。関数であるときは, \(y\)を\(x\)の式で表しなさい。 1 120円のリンゴを\(x\)個買ったときの値段\(y\)円 2 面積が\(x\)cm\(^2\)の三角形の底辺\(y\)cm 3 1辺の長さが\(2x\)cmの正方形の面積\(y\)cm\(^2\) 4 身長\(x\)cmの年齢は\(y\)歳です。 5 1000円を, \(x\)人で分けるときの一人当たりの金額\(y\)円 |
1 最初なので, 丁寧に解説していきます。まずは文字を使わずに, 具体的な値を当てはめて求めていきます。
リンゴ1個の値段は 120円です。
リンゴ2個の値段は 240円です。
リンゴ5個の値段は 600円です。
さて, リンゴ5個の値段をどうやって計算したかというと, ・・・
120×5を計算しました。
では, リンゴ\(x\)個ではどうなるでしょうか。\(120×x=120x\)と書けます。
値段は\(y\)であったので, \(y=120×x=120x\)と書くことができます。
よって, \(y\)は\(x\)の関数です。
2 三角形の面積は底辺×高さ÷2で求めることができます。わかっている数値を当てはめると,
\(x=\displaystyle\frac{y}{2}×\)高さ すなわち, \(y=\displaystyle\frac{2x}{高さ} \)
となり, 高さがわかっていないので, \(x\)を代入しても\(y\)の値は1つに決まりません。よって, これは関数ではありません。
注意
| ちなみに例えば高さが3cmのように示されていれば, \(y=\displaystyle\frac{2}{3}x\)となり, 関数であるといえます。このように, 同じよう問題設定でも, 条件によって関数であったり, 関数でなかったりすることがあります。 |
3 図形の問題では, 実際にかいていくと理解しやすいです。特に周の長さは間違いやすいところがあるので,
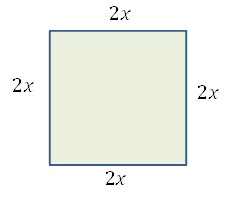
図をかくと一目瞭然ですね。周の長さは\(4×2x=8x\)であるから,
\(y=8x\)となり, 関数であることが分かります。
4 身長が同じでも年齢が違う人がいることから, 身長と年齢は必ずしも対応関係にはなりえません。よって関数ではありません。
5 1000円を\(x\)人で分けるから割り算をします。
\(1000÷x=\displaystyle\frac{1000}{x}\)
よって, \(y=\displaystyle\frac{1000}{x}\) このように\(y\)を\(x\)の形で表すことができたので, 関数です。
まとめ
\(y=(xの文字式)\)の形で書くことができるとき, \(y\)は\(x\)の関数であるといえます。
