正規分布

正規分布

連続型確率変数\(X\)の確率密度関数\(f(x)\)が,　\(m\)は実数,　\(σ\)は正の実数とすると,　\(f(x)=\displaystyle\frac{1}{\sqrt{2\pi}σ}e^{-\frac{(x-m)^2}{2σ^2}}\)で表されるとき,　\(X\)は正規分布\(N(m,　σ^2)\)に従うといい,　\(y=f(x)\)のグラフを正規分布曲線といいます。

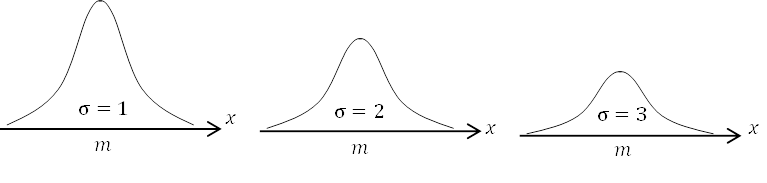
高校数学の範囲内に限れば,　正規分布曲線は出題はほとんどないので,　無視しても構いません。大事なのは,　これを標準化した標準正規分布です。これが頻出なので,　以下を理解していきましょう。

確率変数\(X\)に対して,　\(a,　b\)定数のとき,　確率変数\(Y=aX+b\)で定めた\(Y\)も確率変数となります。正規分布の基本形である平均0,　標準偏差1になるようなYを見つけます。

\(E(Y)=aE(X)+b=am+b,　V(Y)=a^2V(Y)=a^2σ^2\)

まず,　標準偏差を1にするために,　\(a^2σ^2=1,　a=±\displaystyle\frac{1}{σ}\)

次に平均を0にするために,　\( ±\displaystyle\frac{1}{σ} m+b=0,　b=̠∓\displaystyle\frac{m}{σ}\)

複合同順でどちらも成り立ちますが,　このうち,　Xと符号を同じにするのが合理的なので,　\(a>0\)とします。　そのときのYを特にZとおき,　\(Z=\displaystyle\frac{X-m}{σ}\)とします。

この変換のことを標準化といいます。

標準化

確率変数Xが正規分布\(N(m,　σ^2)\)に従うとき,　\(Z=\displaystyle\frac{X-m}{σ}\)と変換することによって,　\(Z\)は標準正規分布\(N(0,　1)\)に従います。このことを標準化といいます。

標準正規分布

正規分布の中で,　特に「平均0,　標準偏差1」である正規分布を標準正規分布\(N(0,　1)\)といいます。 \(N(0,　1)\) において,　確率\(P(0≦Z≦u)=p(u)\) \(p(u)\)の値を表にまとめたものを正規分布表といいます。

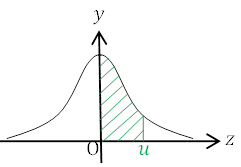
正規分布表の値

\(N(0,　1)\)に従う確率変数の正規分布曲線は直線\(x=0\)に関して対称であり,　次の性質が成り立ちます。 ・\(u>0\)のとき,　\(P(-u≦X≦0)=P(0≦X≦u)\) ・\(P(X≦0)=P(0≦X)=0.5\) 正の実数\(a,　b(a<b)\)に対して, ・\(P(X≦-a)=P(a≦X)=P(0≦X)-P(0≦X≦a)\) ・\(P(a≦X≦b)=P(0≦X≦b)-P(0≦X≦a)\) ・\(P(-a≦X≦b)=P(-a≦X≦0)+P(0≦X≦b)\) \(=P(0≦X≦a)+P(0≦X≦b)\) ・\(P(-a≦X≦-b)=P(-a≦X≦0)-P(-b≦X≦0)\) \(= P(0≦X≦a)-P(0≦X≦b) \)

\(P(Z≦-a)\) \(=P(a≦Z) \) \(=P(0≦Z)-P(0≦Z≦a)\) \(=0.5-p(a)\)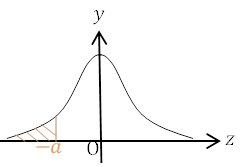
\(P(-a≦Z≦-b)\) \(=P(-a≦Z≦0)-P(-b≦Z≦0)\) \(= P(0≦Z≦a)-P(0≦Z≦b) \) \(=p(a)-p(b)\)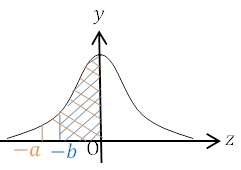
\(P(-a≦Z≦b)\) \(=P(-a≦Z≦0)+P(0≦Z≦b)\) \(=P(0≦Z≦a)+P(0≦Z≦b)\) \(=p(a)+p(b)\)
\(P(a≦Z≦b)\) \(=P(0≦Z≦b)-P(0≦Z≦a)\) \(=p(b)-p(a)\)
\(P(b≦Z) \) \(=P(0≦Z)-P(0≦Z≦b)\) \(=0.5-p(b)\)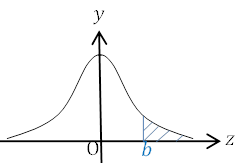