式の計算の利用~図形の性質編~
図形の性質を使った式の計算の利用について解説を行っていきます。図形の性質は苦手な人が多いので, しっかり理解していきましょう。
円の面積や周の長さは忘れている人も多いので, まずはここで確認していきましょう。
目次
復習
| 円の半径を\(r\), 円周率を\(\pi\)とすると, 円の面積=半径×半径×円周率=\(\pi r^2\) 円周の長さ=直径×円周率=\(2\pi r\) |
ここでは, 定期テストで頻出の次の問題を例に考えていきます。
池のまわりの面積と線の長さの関係
| 半径\(r\)mの池のまわりに幅\(a\)mの道がついている。道の真ん中を通る線の長さを\(ℓ\)m, 道の面積を\(S\)m\(^2\)とすると, \(S=aℓ\)となることを証明せよ。ただし, 円周率は\(\pi\)とする。 |
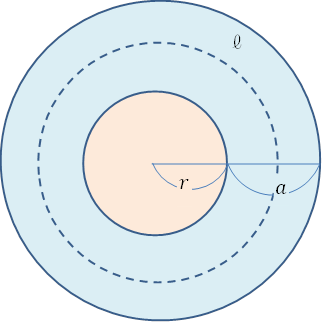
この問題は難しいですか? わからなくなっている原因が文章の長さです。そこで文章を分割して考えます。
文章を読んで多少見慣れない言葉があります。それは, 幅\(a\)mの道, 道の真ん中を通る線の長さ\(ℓ\), 道の面積\(S\)m\(^2\)の3つです。これを1つ1つ分解して考えていきましょう。
幅\(a\)mの道とはどこのことでしょうか? これは簡単です。図の青色のついた部分が幅\(a\)mの道を指します。そしてこの色のついたところの総和が道の面積\(S\)m\(^2\)です。
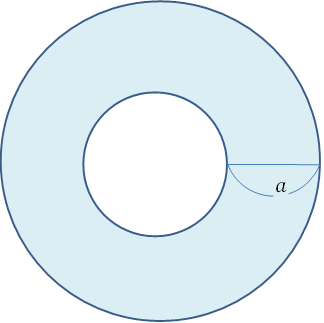
この道の面積はどうやって考えればいいのでしょうか?中が空洞なので, この空洞部分の面積を引いてあげます。
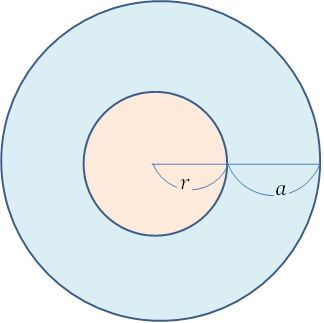
\(-\)
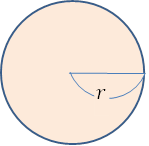
よって, 面積\(S=\pi (a+r)^2-\pi r^2\)で計算することができます。
\(S=\pi (a+r)^2-\pi r^2=\pi (a^2+2ar+r^2)-\pi r^2\)
\(=\pi(a^2+2ar+r^2-r^2)\)
\(=\pi(a^2+2ar)\)
\(=\pi a(a+2r)\)
よって, \(S\)の面積は \(\pi a(a+2r)\)であることが分かりました。
では, 道の真ん中を通る線の長さ\(ℓ\)とはどこのことでしょうか? この長さが少々分かりづらいですが, 下図の点線部分を指します。これは言いかえれば, 半径\(r+\displaystyle\frac{a}{2}\)の円周の長さを指します。
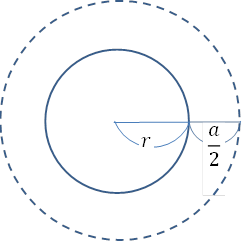
すると, 円の周の長さ\(ℓ\)は, \(ℓ=2\pi ( r+\displaystyle\frac{a}{2}=\pi (a+2r )\)と表すことができます。
最後に, \(S\)と\(ℓ\)の関係式を求めます。
\(S=a×\color{magenta}{\pi (a+2r)}, ℓ=\color{magenta}{\pi (a+2r )} \) であるから, \(ℓ\)を\(S\)に代入すると,
\(S=a×\color{magenta}{\pi(a+2r)}=a×\color{magenta}{ℓ}=aℓ\) (証明終わり)
まとめ
図形の性質を用いた式の計算の利用の問題では, 問題文が長いので, 分割して考えます。見慣れない言葉があったら, 文をよく読んで式化をしていくといいでしょう。面積や周の長さを聞かれることが多いので, 1年や2年で習った図形の性質を見直すようにしていきましょう。
