相似な図形の面積比と体積比の関係
△ABCと△DEFの相似比が1:2であるとします。このとき, △ABCと△DEFの面積比はどうなっているのでしょうか。
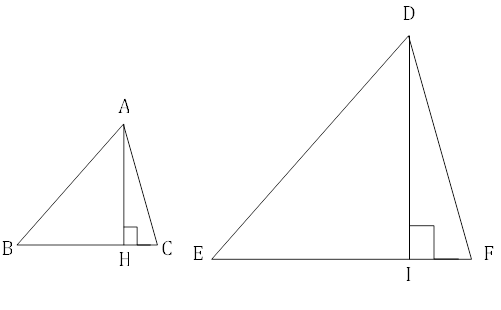
△ABC∽△DEFであるので, BC:EF=1:2であるから, EF=2BC
また, AH:DI=1:2であるから, DI=2AH
△ABCの面積=BC×AH÷2
△DEFの面積=EF×DI÷2=2BC×2AH÷2=4×△ABCの面積
よって, △ABCと△DEFの相似比が1:2のとき, 面積比は1:4になります。面積は底辺×高さというように2つの掛け算で表されるので, 三角形に限らず一般に相似比が\(a:b\)の面積比は次のようになります。
| 相似比が\(a:b\)の図形の面積比は\(a^2:b^2\)になります。 |
相似な図形の面積は, 別々の図形の面積を比べるのではなく, 次のように, 辺や角が共通している三角形同士で行われることが多いので, 次はそのような三角形の面積についてみていきます。
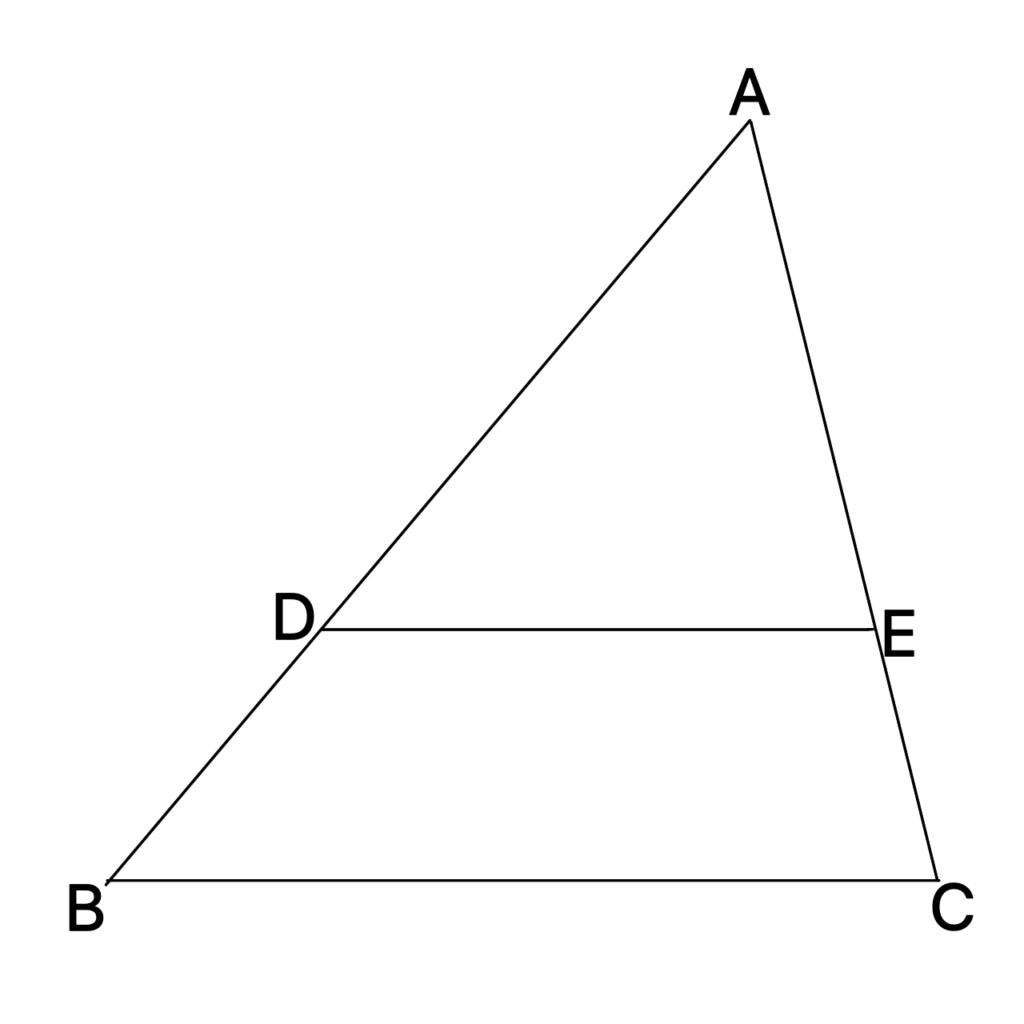
△ABC∽△ADEで, AD:DB=5:2のとき, △ADEの面積と台形DEBCの面積の比を求めなさい。
△ADEと台形DEBCは相似な関係ではないので, 単純に\(5^2:2^2\)と計算することはできません。
△ABCの面積を\(S\), 三角形ADEの面積を\(T\)とおくと, 台形DEBCの面積は△ABCの面積\(S\)から△ADEの面積\(T\)を引くことによって求めることができます。
AD:DB=5:2であるから, AB:AD=7:5である。
よって, △ABC:△ADE\(=S:T=7^2:5^2=49:25\)
ここで, △ADEの面積:台形DEBCの面積\(=T:S-T=25:(49-25)=25:24\)
と, 比の差を使って面積を求めることができるのですが, これは理解できるでしょうか。
比の差を使って面積を求めることができる理由
比の差を使わずに解くとどうなるのでしょうか。具体的な面積がわからないと計算ができないので, △ABCの面積を文字を使って表してみましょう。△ABCの面積を\(k\)とおいてもいいですが, それだと分数が入って少々計算が厄介です。なので, 少しテクニカルですが, 面積を\(49k\)とおいて考えてみます。
△ABCの面積を\(49k\)とおくと, △ADEの面積は,
\(49:25=49k:T\) ∴\(T=25k\)
台形DEBCの面積\(=49k-25k=24k\)
よって, △ADEの面積:台形DEBCの面積\(=25k:24k=25:24\)
このように, 面積の比の差をとることによって, 面積比を求めることができることがわかりました。
まとめ
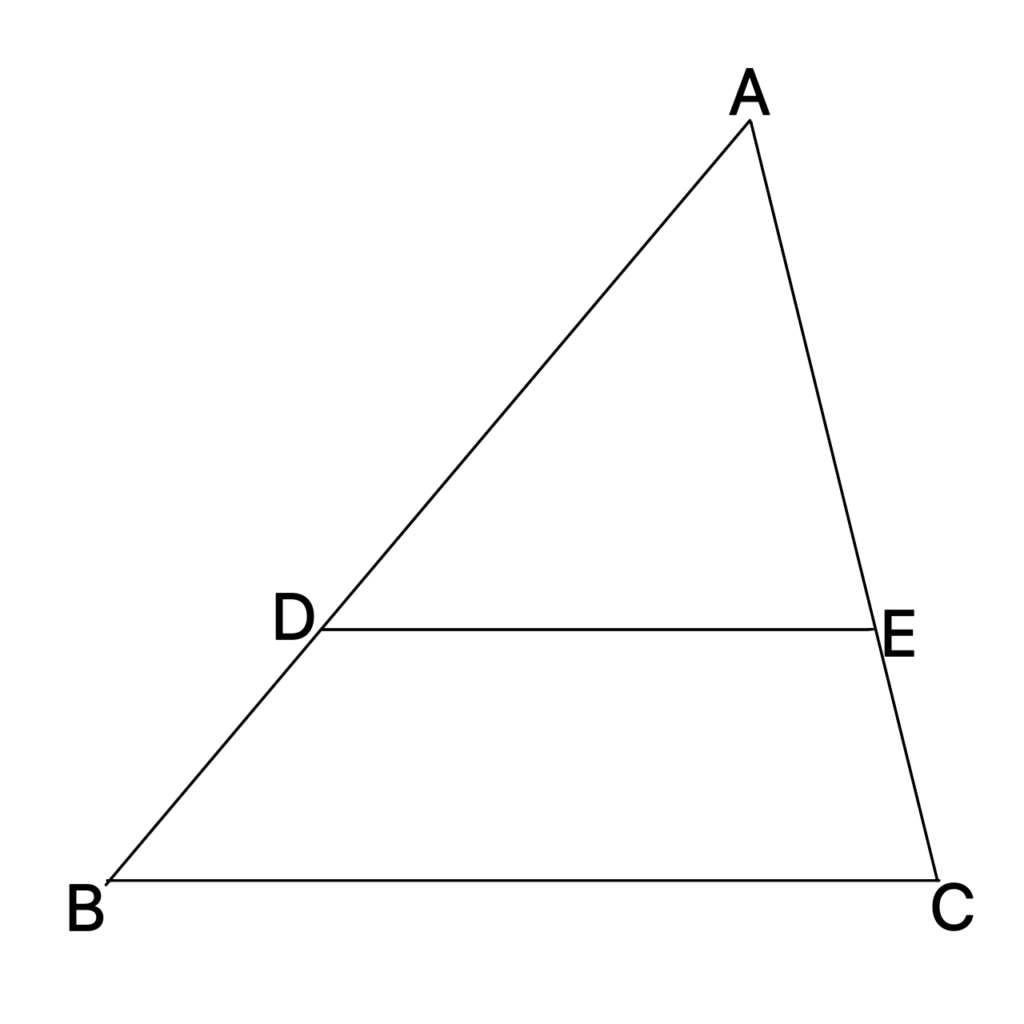
| △ADEの面積を\(S_1\), △ABCの面積を\(S_2\)とすると, △ADEの面積:△ABCのの面積:台形DEBCの面積\(=S_1:S_2:S_2-S_1\) |
