特別な直角三角形の辺の比の関係について

直角三角形の中でも特に2つの三角形を紹介していきます。今は使っていない人もいるかもしれませんが,　三角定規の2組が特別な角度をもっています。

3つの角度が30°,　60°,　90°の直角三角形

3つの角度が30°,　60°,　90°の直角三角形の3辺の長さの比は,　1：\(\sqrt3\)：2です。

これは正三角形を考えることで,　導出できます。まずは具体的な数字で考えていきます。正三角形の辺の長さを2とします。一般的には一辺の長さを1としますが,　この後の計算で分数になってしまうので,　計算の都合上2としています。

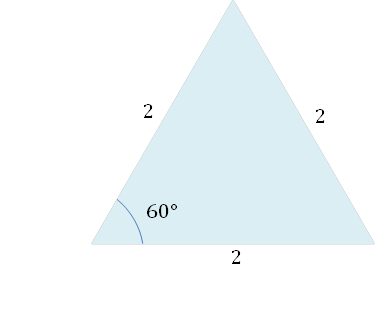
頂点AからBCに下ろした垂線の足をHとすると,　垂線AHはBHを二等分します。これがすぐにわからない場合は,　二等辺三角形の性質を復習してくださいね。

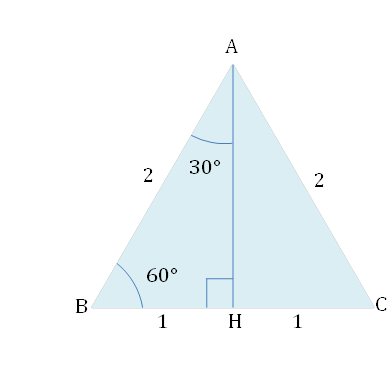
△ABHは直角三角形です。三平方の定理より,　\(1^2+AH^2=2^2\)

\(AH^2=3\)であるから,　AH>0より,　\(AH=\sqrt3\)

これは\(AB=2r\)とすると,　\(BH=r\)であり,　\(AH^2=AB^2-BH^2=4r^2-r^2=3r^2\)

よって,　AH＞0より,　\(AH=\sqrt3r\)

よって,　30°,　60°,　90°の直角三角形の辺の比は,　\(r：\sqrt3r：2r：\sqrt3：2\)であることがわかりました。

45°,　45°,　90°の直角二等辺三角形

45°,　45°,　90°の直角二等辺三角形 の辺の比は,　1：１：\(\sqrt2\)です。

これはそのまま三平方の定理を使うことによって,　導出することができます。

斜辺の長さは正なので,　斜辺以外の辺の長さを\(r\)とすると,　斜辺\(=\sqrt{r^2+r^2}=\sqrt2 r\)

よって,　3辺の比は,　\(r：r：\sqrt2 r=1：１：\sqrt2\)であることがわかりました。

まとめ

特別な直角三角形の比を使うことで,　計算を楽にすることができます。30°,　60°,　90°の直角三角形の辺の比の関係は混同しがちなので,　正三角形と三平方の定理を使って確認するようにしていきましょう。