中点連結定理を使った証明問題
中点連結定理
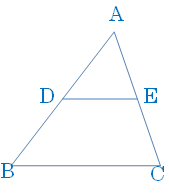
| △ABCの2辺AB, ACの中点をそれぞれD, Eとするとき, DE∥BC かつ DE\(=\displaystyle\frac{1}{2}\)BC |
| 右の図のように, △ABCの内部に点Dをとり, 辺AB, AC, DB, DCの中点をそれぞれ, E, F, G, Hとするとき, 四角形EFGHは平行四辺形であることを証明しなさい。 |
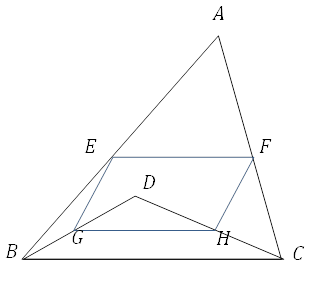
文章の中点というキーワードをもとに, 中点連結定理を利用することを考えます。
△ABCにおいて, 中点連結定理より, EF∥BC, EF\(=\displaystyle\frac{1}{2}BC\)・・・①
△DBCにおいて, 中点連結定理より, GH∥BC, GH\(=\displaystyle\frac{1}{2}BC\)・・・②
①, ②より, EF∥GH, EF=GH
1組の対辺が平行でその長さが等しいから, 四角形EFGHは平行四辺形であることが証明されました。
