中点連結定理について徹底解説

中点連結定理

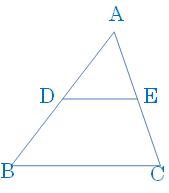
△ABCの辺AB,　AC上の中点をそれぞれD,　Eとするとき, DE∥BC,　DE\(=\displaystyle\frac{1}{2}\)BC

（証明？）

△ADEと△ABCの合同を示していきます。 △ADEと△ABCにおいて, 2点D,　Eはそれぞれ辺AB,　辺ACの中点であるから, AD：AB＝1：2・・・①　 AE：AC＝1：2・・・② 共通な角なので, ∠DAE＝∠BAC・・・③ （注　③については,　∠EAD＝∠CAB　または　∠A＝∠A　とかいてもOKです。） ➀,　➁,　③より2組の辺の比とその間の角がそれぞれ等しいので, △ADE∽△ABC 対応する辺の比は等しいので,　AD：AB＝1：2より,　DE：BC＝1：2 よって,　DE\(=\displaystyle\frac{1}{2}\)BCが示されました。 また,　対応する角は等しいので,　∠ADE＝∠ABC これより,　DEとBCがつくる同位角が等しいことから,　DE∥BCであることが示されました。（証明終わり）

ふっ　三角形の相似条件の一番簡単な方法で求めることができるのか　と思った方はいませんか？

実はこの方法では正しく証明できていません。なぜなら相似条件

それは習う順番にあります。現行の教科書では,　三角形の相似→平行線と線分の比を学習するからです。なので,　相似条件は使えると錯覚してしまいます。

教科書では中点連結定理の紹介だけをして,　証明は行っていないものもあります。

（平行四辺形を用いた証明）

DEの延長線上にDE＝FEとなる点Fをとると,　

DE＝FE・・・④

仮定より,　AE＝CE・・・⑤

④,　⑤より,　対角線がそれぞれの中点で交わるので,　四角形ADCFは平行四辺形である。

よって,　AD∥FC・・・⑥,　AD＝FC・・・⑦

⑥より,　DB∥FC・・・⑧

仮定より,　AD＝DBであるから,　⑦と合わせて,　DB＝FC・・・⑨

⑧,　⑨より,　1組の対辺が平行でその長さが等しいので,　四角形DBCFは平行四辺形である。

よって,　DE∥BC

また,　DE\(＝\displaystyle\frac{1}{2}\)DF=\(\displaystyle\frac{1}{2}\)BC

（等積変形を使った証明）

仮定により　

AD＝DB　であるから,　△ADE＝△BDE・・・⑩

AE＝EC　であるから,　△ADE＝△DCE・・・⑪

⑩,　⑪より,　△BDE＝△DCE・・・⑫

⑫と,　辺DEは共通な辺であるから,　DE∥BC・・・⑬

また,　△ABE＝2×△DBE,　△ABD＝△BECより,

△DBE：△BEC＝1：2

よって,　DE：BC＝1：2　（証明終わり）

今後中点連結定理はよく使うので,　しっかり理解していきましょう。