座標平面上の2点間の距離の求め方
dora座標平面上の2点間の距離の求め方
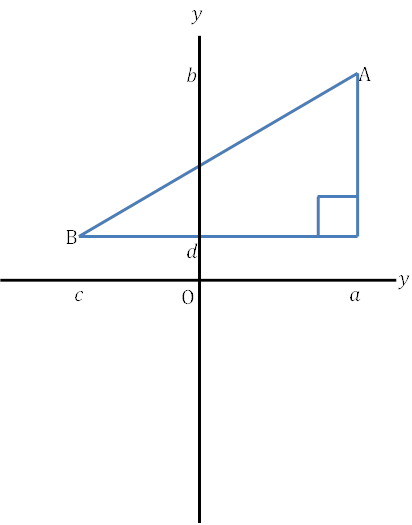
| 2点を結ぶ線分を斜辺とし, x軸に平行な辺とy軸に平行な辺をもつ直角三角形をつくり, 三平方の定理を使います。 2点A(a, b), B(c, d)間の距離ABについて, AB^2=(a-c)^2+(b-d)^2で求めることができます。 |
例 2点A（－1, 1）とB（2, －4）の距離を求めなさい。
AB^2=\{(-1)-2\}^2+\{1-(-4)\}^2=9+25=34
AB>0なので, AB=\sqrt{34}
